

Josh is hoping to get an A in his college algebra class. He has scores of 75, 82, 95, 91, and 94 on his first five tests. Only the final exam remains, and the maximum of points that can be earned is 100. Is it possible for Josh to end the course with an A? A simple linear equation will give Josh his answer.
Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus a charge per minute of talk-time; it costs a widget manufacturer a certain amount to produce x widgets per month plus monthly operating charges; a car rental company charges a daily fee plus an amount per mile driven. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.
To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let us use the car rental example above. In this case, a known cost, such as $0.10/mi, is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write[latex]\,0.10x.\,[/latex]This expression represents a variable cost because it changes according to the number of miles driven.
If a quantity is independent of a variable, we usually just add or subtract it, according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges $0.10/mi plus a daily fee of $50. We can use these quantities to model an equation that can be used to find the daily car rental cost[latex]\,C.[/latex]
[latex]C=0.10x+50[/latex]When dealing with real-world applications, there are certain expressions that we can translate directly into math. Table 1 lists some common verbal expressions and their equivalent mathematical expressions.
| Verbal | Translation to Math Operations |
|---|---|
| One number exceeds another by a | [latex]x,\text\,x+a[/latex] |
| Twice a number | [latex]2x[/latex] |
| One number is a more than another number | [latex]x,\text\,x+a[/latex] |
| One number is a less than twice another number | [latex]x,\,2x-a[/latex] |
| The product of a number and a, decreased by b | [latex]ax-b[/latex] |
| The quotient of a number and the number plus a is three times the number | [latex]\frac=3x[/latex] |
| The product of three times a number and the number decreased by b is c | [latex]3x\left(x-b\right)=c[/latex] |
Given a real-world problem, model a linear equation to fit it.
Find a linear equation to solve for the following unknown quantities: One number exceeds another number by[latex]\,17\,[/latex]and their sum is[latex]\,31.\,[/latex]Find the two numbers.
Show SolutionLet[latex]\,x\,[/latex]equal the first number. Then, as the second number exceeds the first by 17, we can write the second number as[latex]\,x+17.\,[/latex]The sum of the two numbers is 31. We usually interpret the word is as an equal sign.
[latex]\begin
The two numbers are[latex]\,7\,[/latex]and[latex]\,24.[/latex]
Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is[latex]\,36,[/latex] find the numbers.
Show SolutionThere are two cell phone companies that offer different packages. Company A charges a monthly service fee of $34 plus $.05/min talk-time. Company B charges a monthly service fee of $40 plus $.04/min talk-time.
[latex]\begin
[latex]\begin
[latex]\begin
[latex]\begin
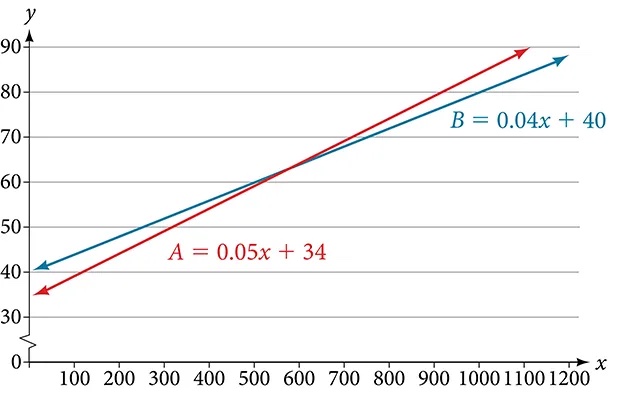
Therefore, a monthly average of 600 talk-time minutes renders the plans equal. See Figure 2.
Find a linear equation to model this real-world application: It costs ABC electronics company $2.50 per unit to produce a part used in a popular brand of desktop computers. The company has monthly operating expenses of $350 for utilities and $3,300 for salaries. What are the company’s monthly expenses?
Show SolutionMany applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region,[latex]\,A=LW;[/latex] the perimeter of a rectangle,[latex]\,P=2L+2W;[/latex] and the volume of a rectangular solid,[latex]\,V=LWH.\,[/latex]When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.
It takes Andrew 30 min to drive to work in the morning. He drives home using the same route, but it takes 10 min longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?
Show SolutionThis is a distance problem, so we can use the formula[latex]\,d=rt,[/latex]where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.
First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or[latex]\,\frac\,[/latex]h at rate[latex]\,r.\,[/latex]His drive home takes 40 min, or[latex]\,\frac\,[/latex]h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance[latex]\,d.\,[/latex]A table, such as Figure 3, is often helpful for keeping track of information in these types of problems.
| [latex]d[/latex] | [latex]r[/latex] | [latex]t[/latex] | |
|---|---|---|---|
| To Work | [latex]d[/latex] | [latex]r[/latex] | [latex]\frac[/latex] |
| To Home | [latex]d[/latex] | [latex]r-10[/latex] | [latex]\frac[/latex] |
Write two equations, one for each trip.
As both equations equal the same distance, we set them equal to each other and solve for r.
[latex]\begin
We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.
[latex]\beginThe distance between home and work is 20 mi.
Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for[latex]\,r.[/latex]
[latex]\begin
On Saturday morning, it took Jennifer 3.6 h to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 h to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?
Show SolutionThe perimeter of a rectangular outdoor patio is[latex]\,54\,[/latex]ft. The length is[latex]\,3\,[/latex]ft greater than the width. What are the dimensions of the patio?
Show SolutionThe perimeter formula is standard:[latex]\,P=2L+2W.\,[/latex]We have two unknown quantities, length and width. However, we can write the length in terms of the width as[latex]\,L=W+3.\,[/latex]Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides, as in Figure 3.
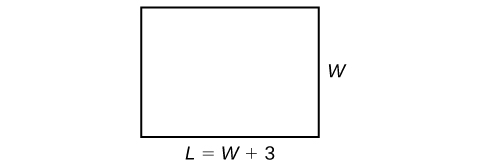
Now we can solve for the width and then calculate the length.
[latex]\begin
The dimensions are[latex]\,L=15\,[/latex]ft and[latex]\,W=12\,[/latex]ft.
Find the dimensions of a rectangle given that the perimeter is[latex]\,110\,[/latex]cm and the length is 1 cm more than twice the width.
Show SolutionThe perimeter of a tablet of graph paper is 48 in. The length is[latex]\,6\,[/latex]in. more than the width. Find the area of the graph paper.
Show SolutionThe standard formula for area is[latex]\,A=LW;[/latex] however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.
We know that the length is 6 in. more than the width, so we can write length as[latex]\,L=W+6.\,[/latex]Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.
[latex]\begin
Now, we find the area given the dimensions of[latex]\,L=15\,[/latex]in. and[latex]\,W=9\,[/latex]in.
[latex]\begin
The area is[latex]\,135\,[/latex]in. 2 .
A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft 2 of new carpeting should be ordered?
Show SolutionFind the dimensions of a shipping box given that the length is twice the width, the height is[latex]\,8\,[/latex]inches, and the volume is 1,600 in.3.
Show SolutionThe formula for the volume of a box is given as[latex]\,V=LWH,[/latex] the product of length, width, and height. We are given that[latex]\,L=2W[/latex] and[latex]\,H=8.\,[/latex]The volume is[latex]\,1,600\,[/latex]cubic inches.
[latex]\begin
The dimensions are[latex]\,L=20\,[/latex]in.,[latex]\,W=10\,[/latex]in., and[latex]\,H=8\,[/latex]in.
Note that the square root of[latex]\,^\,[/latex]would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.
Answers may vary. Possible answers: We should define in words what our variable is representing. We should declare the variable. A heading.
For the following exercises, use the information to find a linear algebraic equation model to use to answer the question being asked.
For the following exercises, use this scenario: Two different telephone carriers offer the following plans that a person is considering. Company A has a monthly fee of $20 and charges of $.05/min for calls. Company B has a monthly fee of $5 and charges $.10/min for calls.
For the following exercises, use this scenario: A wireless carrier offers the following plans that a person is considering. The Family Plan: $90 monthly fee, unlimited talk and text on up to 8 lines, and data charges of $40 for each device for up to 2 GB of data per device. The Mobile Share Plan: $120 monthly fee for up to 10 devices, unlimited talk and text for all the lines, and data charges of $35 for each device up to a shared total of 10 GB of data. Use[latex]\,P\,[/latex]for the number of devices that need data plans as part of their cost.
For exercises 17 and 18, use this scenario: A retired woman has $50,000 to invest but needs to make $6,000 a year from the interest to meet certain living expenses. One bond investment pays 15% annual interest. The rest of it she wants to put in a CD that pays 7%.
She traveled for 2 h at 20 mi/h, or 40 miles.
$5,000 at 8% and $15,000 at 12%
For the following exercises, use this scenario: A truck rental agency offers two kinds of plans. Plan A charges $75/wk plus $.10/mi driven. Plan B charges $100/wk plus $.05/mi driven.